Абстракция
/Тред
придуманная человеком хуйня что бы считать предметы (На самом деел тоже нахуй не надо, ведь человек почти всегда точно определяет на глаз, типа мало, много, норм, дохуя). Дальше человек придумал думать наперед (что очень очень зря), тем самым допер в своих же ебучих в абстракциях до i, всей ирациональщины и прочей хуйни. хотя мог этого не делать.
Два говна мамонта, анон. Реально помог разобраться в предмете.
>Дальше человек придумал думать наперед (что очень очень зря), тем самым допер в своих же ебучих в абстракциях до i
Прикол в том, что либо раньше у числа были другие свойства(или вообще это был другой объект), либо изначально числа были не про счёт, а про интерпретацию счёта. И вот то, что ты называешь думать наперёд, сделало либо трансформацию числа или дало понять, что число это про другое.
А вот, что сейчас такое число непонятно никому.
Бамп
Это такое абстрактное свойство предметов
>число
выдуманная хуйня бибизяками чтобы можно было бананы считать
Число — это одно из основных понятий математики, используемое для количественной характеристики, сравнения и нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры и символы математических операций.
### Основные числовые множества:
1. Натуральные числа (N) — используются для счета и нумерации объектов.
2. Целые числа (Z) — включают натуральные числа, ноль и отрицательные числа.
3. Рациональные числа (Q) — включают целые и дробные числа, которые можно представить в виде отношения двух целых чисел.
4. Иррациональные числа — не могут быть выражены в виде отношения двух целых чисел, например, √2.
5. Действительные числа (R) — включают рациональные и иррациональные числа.
6. Комплексные числа (C) — включают действительные числа и мнимые числа, которые используются в алгебре и анализе.
### История развития понятия числа:
- Доисторические времена: Считать предметы человек умел ещё в глубокой древности, тогда и возникло понятие натурального числа.
- Появление письменности: Возможности воспроизведения чисел значительно увеличились с появлением письменности.
- Появление арифметики: Со временем начинают применяться действия над числами, сначала сложение и вычитание, позже умножение и деление.
- Введение отрицательных чисел: Отрицательные числа были введены для решения алгебраических уравнений.
- Введение действительных чисел: В XVII веке были разработаны методы изучения непрерывных процессов и методы приближённых вычислений.
- Введение комплексных чисел: С развитием алгебры возникла необходимость введения комплексных чисел.
### Философский аспект:
Платон и неоплатоники считали числа основой упорядоченности мира, придающей вещам меру и определённость. Аристотель, напротив, утверждал, что числа являются результатом рассмотрения реально существующих вещей с точки зрения их количества.
Таким образом, число — это фундаментальное понятие, которое прошло долгий путь развития от простых методов счёта до сложных математических теорий и философских концепций.
То ест, число находится в предметах? А если нет, то какого хуя свойство предмета не принадлежит предмету?
Бамп
Бамп
>Покажи объекты количеством в i.
Какое еще нахуй количество i, это множитель для оси у для наглядной записи. Иди нахуй, долбаеб
>Какое еще нахуй количество i, это множитель для оси у для наглядной записи.
В том то и прикол, что i не количество. Иди нахуй неумеющий читать, далбоёб
Число -- это элемент множества чисел
Множество натуральных чисел задаётся аксиоматикоц пеано, далее расширяется до множества целых, рациональных, действительных, комплексных
Множество натуральных чисел задаётся аксиоматикоц пеано, далее расширяется до множества целых, рациональных, действительных, комплексных
ПАСМАТРИТЕ Я ДАЛБАЕБ
@
ЧЕЛ ТЫ ДАЛБАЕБ
@
НЕЕЕЕТ ЭТО БЫЛ ТРОЛЛИНГ Я НЕ ДАЛБАЕБ
>Число -- это элемент множества чисел
А долбаёб — это элемент множества долбаёбов.
Дальше что?
>Дальше что?
Ничего. А что хотел-то?
Это троллинг?
Зачем отвечать на ответку к инб4? Там про это сказано.
Или ты хотел, чтоб в опе было написано:"покажите предметы количеством числа 0+1*i"?
> пук
Чё сказать хотел, или тред чисто тупостью потроллить? Убери второе слово число, если смущает
У тебя определение зациклинное. Понимаешь.
Определение ничего не говорит об определяемом объекте. Этого объекта может даже и не существовать.
Определение не определяет. Вот что я хотел сказать.
>Убери второе слово число, если смущает
Число — элемент множества
Кусок говна — элемент множества кусков говна
Кусок говна —число.
Число -- элемент множества.
Берется аксиоматика пеано, получается множество N, далее расширяется до Z, Q, R, C и сколько угодно далее -- в зависимости от задачи
Элементы этих множеств называются числами
Нахуя я отвечаю, ты же реально троллишь
>Число -- элемент множества
Какого множества? Множества чего? У тебя определение не выполняет функции определения.
>Берется аксиоматика пеано
Она работает с числами. А числа это что? А хуй его знает. Элемент какого-то или любого множества. А значит, число может быть и элементом множества калла и элементом множества мочи. И они хоть как-то определяют число.
А число — элемент множества чисел. Не определяет число, т. к. чтоб определить число нужно знать что такое множество чисел. А чтоб знать что такое множество чисел, нужно знать что такое число.
Число - абстрактный обьект, используется в отношении других обьектов для описания их количества.
Мера определения хуев в жопе
>Покажи объекты количеством в i.
Если ты имеешь ввиду мнимую единицу, то представить её можно следующим образом.
Допустим, что ты взял в долг квадратный участок земли площадью в 25 условных единиц и продал его.
Теперь на твоем счету квадратный участок земли площадью -25 условных единиц. Какая длина стороны этого участка?
sqrt(-25) = 5i.
>Теперь на твоем счету квадратный участок земли площадью -25 условных единиц
Площадь с отрицательной величиной? Серьёзно.
Я могу чуть-чуть по другому интерпретировать это. Я взял в долг квадратный участок земли со стороной 5. Я продал этот участок. На моём счету квадратный участок площадью -52, то есть со стороной в 5.
Именно поэтому я написал покажи это количество, а не дай интерпретацию того или иного.
Ну оно находится в идее предмета скорее
Число это мера измерения.
/tread
/tread
А идея где? Если в сознании человека, то претензия остаётся. Если не в сознании, то где ещё?
Некоего обще признанное понятие, позволяющее нам различать множества абстрактных вещей.
Измерения чего?
>различать множества абстрактных вещей.
Можно абстрагировать в любом направлении. То есть будут такие множества, где числа неприменимы.
Например, множество цветов(цвет объекта=/=объект, а значит мы абстрагируемся от объекта) различно множеству вкуса(то же самое, что и с цветами).
Ну бля, физически нигде
Но заметь, вот у нас есть красный цветок, красная кровь, красный помидор. И во всех них присутствует идея красности. В каждом из них в той или иной мере, но нигде не полностью. Где содержится "красность" сама по себе? Ну вот там и числа.
В красной части спектра красность содержится, соответствует определенному диапазону длины волн. Этот диапазон воспринимается человеком как оттенки красного. А еще у красного цвета есть условный номер, кстати это 1.
А спектр где содержится? Найс объяснять одну выдуманную штуку другой
>натуральные числа
Аксиоматика Пеано.
<скип>
>вещественные числа
Что-то там про, хуё-моё, последовательности и пределы.
>числа в целом
Не имеет аналитического определения, только остенсивное: числа - это любая хрень, которая по тем или иным причинам напоминает говорящему натуральные и/или вещественные числа и о которой в данный момент хочется попиздить.
>Она работает с числами.
Схуяли? Это индуктивное определение одних штук через уже определённые штуки. Числа тебе для этого нахуй не нужны, нужно только понятие "шага", "действия" или типа того. Потом уже можно вернуться к этой ебале с теоремой Тарского за плечами и конкретно её выебать, но для первоначального определения это нахрен не нужно.
Я бы так сказал. Число - это элемент множества изосорфного множеству комплексных чисел(все свойства и операции описаны).
Какой из этих цветов - первый уже не красный, умник?
У тебя в голове почему-то только красный и не красный, а по сути переход плавный. Какой решишь что первый не красный тот и будет для тебя субъективно не красным. Для кого-то еще это может быть другой некрасный. Видимо первый некрасный этот тот который не красный для большинства наблюдателей.
Хуй знает что тут происходит, но из этих самый красный - второй, первый ближе к малиновому а все остальное - скорее оттенки мандарина.
Самый красный из них первый, я со спектра брал.
Ну так где идея красного?
В свете. Ты даже можешь его увидеть. Радуга, например.
Два долбоеба. i2 = -1. А значит i = √-1. Учите матчасть.
>Самый красный из них первый, я со спектра брал.
Понятно, ну до тру красного ему далековато.
если что - мимоход
Так мы тут будем долго хуйней страдать. Давай сюда развернутое определение идеи как таковой в твоем понимании.
Это абстракт для выражения меры. То, что ты своими глазками там чего-то себе представить не можешь, не означает, что теории неверны или что-либо ещё.
Ты можешь без проблем КАЖДОМУ цвету (оттенку) задать взаимно соответствующее натуральное число, так как их бесконечное множество.
Что ты подразумеваешь под фразой "уже не красный"?
Можешь также сделать и с со словами и буквами. Буквы и слова числа?
>Не имеет аналитического определения
С чего ты взял?
>Схуяли?
Аксиоматика Пеано просто пытается формализовать арифметику через логику предикатов первого порядка. Формализация =/= определение, как минимум любое(даже возможное), что выходит за пределы этой аксиоматики и называется числом, доказывает, что эта аксиоматика не определения числа. Например, арифметика второго порядка.
>Числа тебе для этого нахуй не нужны
Не нужны?
Если число то, что формализуется аксиомами Пеано, то существуют некоторые множества вещей(в том числе и возможных), которые могут формализоваться этими аксиомами, но не является числами. Ведь формализованние всего лишь интерпретация.
Потому то, нужно сначала определить число.
>Не имеет аналитического определения
С чего ты взял?
>Схуяли?
Аксиоматика Пеано просто пытается формализовать арифметику через логику предикатов первого порядка. Формализация =/= определение, как минимум любое(даже возможное), что выходит за пределы этой аксиоматики и называется числом, доказывает, что эта аксиоматика не определения числа. Например, арифметика второго порядка.
>Числа тебе для этого нахуй не нужны
Не нужны?
Если число то, что формализуется аксиомами Пеано, то существуют некоторые множества вещей(в том числе и возможных), которые могут формализоваться этими аксиомами, но не является числами. Ведь формализованние всего лишь интерпретация.
Потому то, нужно сначала определить число.
>Даём определения
Наиболее абстрактное выражение количества.
Наиболее абстрактное выражение количества.
>То, что ты своими глазками там чего-то себе представить не можешь, не означает, что теории неверны или что-либо ещё.
И не означает, что теория верна.
Только проблема в том, что мы некоторые числа могут быть использованы для меры, только когда интерпретируем их определённым образом, отличным от их определения относительно других чисел. Иначе ими мы не можем мерить.
>С чего ты взял?
Из общих соображений. Люди все разные, у всех свои вкусы и интересы. Ну не обобщишь ты аналитически определение числа так, чтобы опрятненько вобрать в себя все мыслимые интуитиции касательно чисел, числимости и всего такого. Лопнет. Забрызгает. У меня нет строгого доказательства невозможности дать такое определение, но анус ставлю. Да и нафига?
>множества
Этого слова я бы избегал особо тщательно. Тебе не видно, но я на всякий случай даже тупую рожу скорчил и пустил слюну из уголка рта, когда его копипастил. Какие такие множества? Не, не слышал.
>существуют вещи, которые могут формализоваться этими аксиомами, но не являютя числами
Или что? Постулирую: если что-то конструируется как s(s(s(s(s(z))))), то это оно и есть с точностью до поебатьморфизма и положитьтопии. Не нравится - вызывай мусоров.
Это не «что», а «сколько».
/theead
>Постулирую: если что-то конструируется как s(s(s(s(s(z))))), то это оно и есть с точностью до поебатьморфизма и положитьтопии
Констатировать как s(s(s(s(s(z))))) можно всё что угодно. Ты постулируешь, что каждый предмет и есть другие предметы.
Это абстрактное понятие из математики. В природе не существует.

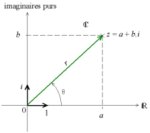
















ИТТ обсуждаем объект "число". Даём определения, обсуждаем его свойства и историю.
>инб4: число — количество.
Покажи объекты количеством в i.